
안녕하세요 :)
오늘은 신경망 기반의 딥러닝에 대한 기본적인 이야기를 해보려고 합니다.
주어진 데이터를 스스로 학습이 가능하다는 점이 신경망 기반의 딥러닝의 장점이라고 할 수 있는데요.
신경망을 설명하려면 뉴런에 대해서 먼저 간단하게 이해해야 합니다.
뉴런 (neuron)

뉴런의 기본적인 특징을 먼저 살펴보겠습니다.
- 다수의 뉴런들로 네트워크를 구성합니다.
- 입력된 값의 합이 임계값을 넘지 않으면 해당 뉴런은 반응하지 않습니다.
- 입력된 값의 합이 임계값을 넘으면, 다른 뉴런에 일정 강도의 신호를 전달합니다.
- 여러 뉴런에서 전달되는 신호의 합은 가중치가 각각 다릅니다.
쉽게 말하면, 서로 다른 뉴런으로부터 신호를 받아 가중치에 따라 입력된 값이 임계값을 넘는 경우 연결된 또 다른 뉴런들에게 전달되는 구조입니다.
이러한 뉴런의 구조를 살펴보겠습니다. 뉴런은 크게 신경세포체, 수상돌기, 축삭으로 이루어져 있습니다.
- 신경세포체 (A) : 입력 신호를 전달하는 역할을 수행합니다. 여러 뉴런에서 받은 신호의 합이 임계값을 넘기지 못하면 신경세포체는 입력 신호를 무시하고, 임계값을 넘기는 경우, 다른 뉴런에 신호를 전달합니다. 전달되는 신호 y는 각각 0 (신호가 없음) 또는 1 (신호가 있음)의 값을 갖게 됩니다.
- 수상돌기 (B) : 신호를 입력받습니다.
- 축삭 (C) : 축삭의 끝의 시냅스를 통해 다른 뉴런에 신호를 전달합니다. 이 때, 신호의 합을 뉴런의 입력 신호로 사용합니다. 입력신호 x는 각각 0 (입력 업음) 또는 1 (입력 있음)의 값을 갖게 됩니다.

뉴런의 입력으로 사용되는 신호의 합에 대해서 조금 더 이야기해보겠습니다.
한 뉴련에 3개의 서로 다른 뉴런이 신호를 보낸다고 했을 때, 각각의 신호를 x1, x2, x3이라고 가정해 봅시다.
뉴런의 출력(y) 가 1인 경우와, 0인 경우를 수식으로 나타내면 다음과 같습니다.

여기서 Θ는 각 뉴런의 고유 임계값입니다.
위의 수식을 그래프로 나타내면 다음과 같습니다.

위와 같은 함수를 "단위 계단 함수"라고 합니다.
위의 함수를 일반화하면 다음과 같이 표현할 수 있습니다.
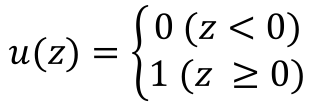
위의 식에서 z를 뉴런의 가중 입력이라고 하면,

z의 값은 위와 같이 정할 수 있습니다.
위의 식을 그림으로 다시 표현하면 다음과 같습니다.

실제 뉴런이 아닌, 추상화한 뉴런을 유닛(unit)이라고 부릅니다.
유닛은 실제 뉴런과 다르게 출력 신호를 0과 1로 제한하지 않는다는 것입니다.

실제 뉴련 연산에서 사용한 u(z) 대신 새로운 함수 a()를 사용하게 됩니다.
a()를 활성화 함수라고 부르는데, 사용자가 직접 정의할 수 있습니다.
대표적으로는 sigmoid 함수가 있습니다.
Sigmoid 함수
시그모이드(sigmoid) 함수에 대해서 간단하게 알아보겠습니다.


시그모이드 함수는 가장 대표적인 활성화 함수라고 할 수 있습니다.
시그모이드 함수에는 크게 2가지 특징이 있습니다.
- 모든 출력은 0보다 크고 1 보다 작습니다.
- 모든 구간에서 미분이 가능합니다.
시그모이드 함수의 결과가 0에 가까우면 흥분도가 낮고, 1에 가까우면 흥분도가 높다고 할 수 있습니다.
편향 (bias)
편향 (bias)는 신호 출력 여부를 결정하는 임계값입니다.
편향 값이 크면 둔감, 작으면 민감하게 반응합니다.
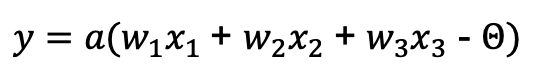
위의 식에서 -Θ 로 표현되는 값을 b로 치환해서 식을 수정하면 다음과 같이 표현할 수 있습니다.

위와 동일하게 함수 a() 의 인자로 넘어가는 값은 유닛의 가중 입력(z)입니다.
가중 입력은 다음과 같이 벡터의 내적으로도 표현이 가능합니다.

계층형 신경망
기본적인 신경망 중에는 계층형 신경망과 합성곱 신경망(Convolutional Neural Network, CNN)이 있습니다.
먼저 계층형 신경망에 대해서 알아보겠습니다.
계층형 신경망은 크게 입력층, 은닉층, 출력층으로 구성됩니다.
- 입력층 : 입력값을 그대로 출력하는 층입니다. 항등 함수(identity function)와 동일하게 동작합니다.
- 은닉층 : 신경망에서 실제 정보를 처리하는 부분입니다. 특징을 추출하는 역할을 수행합니다.
- 출력층 : 신경망에서 계산한 결과를 출력합니다.
각 층은 한 개 이상의 유닛으로 구성됩니다.
계층형 신경망 중 입력층의 유닛 전부가 중간층의 유닛 전부에 신호를 보내는 경우 완전 연결 계층(fully connected layer)라고 합니다.
신경망은 명확한 기준이 없는 문제를 네트워크의 판단으로 해결합니다.
계층형 신경망에서 결과를 예측하는 과정을 간단하게 설명하면 다음과 같습니다.
- 입력층에서 입력받은 값을 그대로 전달합니다.
- 값을 전달받은 층 (은닉층)에서는 건내받은 값을 종합해서, 종합한 값(가중 입력)에 따라 반응합니다.
- 유닛 사이에 관계가 존재합니다. 유닛 사이에 관계가 좋은 경우, 전달받은 값을 더 적극 반영합니다. 관계를 가중치(weight)라고 표현합니다.
- 전달받은 신호를 선명하게 하고, 불필요한 정보를 차단하기 위해 편향 (bias)를 사용합니다.
- 신경망 전체의 가중치를 기반으로 입력값에 대해 결과를 예측합니다.
학습
신경망의 모든 가중치(weight)와 편향(bias)이 올바른 결과를 도출하는지 검증해야 합니다.
올바른 결과가 나오지 않는 경우 가중치와 편향의 값을 조금씩 수정하면서 올바른 결과를 도출하는 신경망을 구성해야 합니다.
파라미터 (parameter, 가중치와 편향)를 결정하는 방법은 크게 지도 학습과 비지도 학습이 있습니다.
지도 학습은 파라미터를 정하기 위해 미리 주어지는 데이터가 존재합니다.
학습은 해당 데이터를 이용해서 신경망의 예측값과 주어진 정답 사이의 오차를 계산해서 오차를 최소화하는 파라미터를 구하는 과정을 말합니다.
학습에 대한 이야기는 다른 게시물에서 다시 다뤄보도록 하겠습니다 :)
 |
|
<처음 배우는 딥러닝 수학>을 읽으면서 개인적으로 정리한 내용입니다.
제가 잘못 이해했거나, 수정이 필요한 부분에 대한 피드백은 언제든지 환영입니다.
감사합니다 :)
'필기 노트 > 처음 배우는 딥러닝 수학' 카테고리의 다른 글
| [딥러닝 기초] 오차역전법 (back-propagation) (0) | 2020.07.10 |
|---|---|
| [딥러닝 기초] 신경망과 학습 (0) | 2020.07.09 |
| [딥러닝 기초] 경사하강법과 회귀분석 (0) | 2020.07.09 |
| [딥러닝 기초] 딥러닝 수학 - 2 : 행렬, 미분 (0) | 2020.07.06 |
| [딥러닝 기초] 딥러닝 수학 - 1 : 함수, 수열, 벡터 (0) | 2020.07.01 |




댓글