
안녕하세요 :)
오늘은 구체적인 딥러닝 이야기를 하기에 앞서, 딥러닝을 이해하는데 필요한 수학적인 내용을 다뤄볼까 합니다.
크게 함수, 수열, 벡터에 대한 내용을 다뤄보겠습니다.
1. 함수
1차 함수
가장 기본적인 1차 함수에 대해서 알아보겠습니다.
일차 함수는 기본적으로 다음과 같은 형식으로 구성될 수 있습니다.

위 식은 독립 변수가 1개인 가장 단순한 형태의 1차 함수입니다.
다음과 같이 2개의 독립 변수로 구성된 1차 함수를 생성할 수도 있습니다.
이 때, y는 x1, x2와 "1차 함수 관계"라고 표현합니다.

※ 독립 변수와 종속 변수
x가 주어졌을 때, y의 값이 정해진다면,
x는 독립변수, y는 종속 변수라고 할 수 있습니다.
앞서 배운 신경망의 가중입력은 1차 함수 관계로 표현할 수 있습니다.
가중치(w1, w2, w3)와 편향(b)을 파라미터로 생각했을 때, x1, x2, x3의 값이 입력값으로 고정이면
가중 입력 z는 w1, w2, w3, b 와 1차 함수 관계에 있다고 할 수 있습니다.

2차 함수
2차 함수는 포물선의 형태로 그래프가 그려집니다.
가장 단순한 2차 함수 형태는 다음과 같습니다.

a가 양수면 아래로 볼록한 그래프가 형성되므로 최소값이 존재합니다.
다음과 같이 독립 변수가 2개인 2차 함수도 생성할 수 있습니다.

지수 함수
지수 함수는 다음과 같이 나타낼 수 있습니다.

이 때, a는 지수 함수의 밑(base)라고 합니다.
지수 함수의 밑을 지연상수로 지정하는 경우도 있습니다.
자연상수 e = 2.7181828... 의 값을 갖습니다.
자연상수를 사용하는 지수 함수는 앞선 게시물에서 잠깐 언급한 시그모이드(sigmoid) 함수에서 사용됩니다.

시그모이드 함수의 가장 큰 특징은 다음과 같습니다.
- 모든 구간에서 미분이 가능하다
- 함수값이 0과 1사이에서 나타나기 때문에, 확률을 계산할 수 있다.
정규분포의 활률밀도함수
신경망을 구성할 때, 초기 가중치 및 편향을 지정해야 합니다.
이 때, 우리가 초기값으로 자주 사용하는 값은 정규분포 난수입니다.
정규분포를 따르는 난수를 초기값으로 지정하면 보다 좋은 성능을 낼 수 있습니다.
확률밀도함수 f(x)를 따르는 확률 분포를 정규분포라고 하는데, 확률밀도함수 f(x)는 다음과 같습니다.

위의 식에서 μ는 평균값을, σ는 표준편차를 나타냅니다.
확률밀도함수 중 평균값(μ)이 0이고, 표준편차(σ)가 1인 경우를 표준정규분포라고 부릅니다.
2. 수열과 점화식
수열
수열은 숫자의 열을 의미합니다. 이 때, 정렬한 숫자 하나하나를 항이라고 부릅니다.
그러므로 n번째 항을 n항이라고 부르고 an이라고 표현합니다.
수열 중 유한개의 항을 보유한 수열을 유한 수열이라고 부릅니다.
유한수열에서 마지막 항은 말항(final term)이라고 합니다.
신경망에서 유닛의 가중입력과 출력을 수열로 간주합니다.

점화식
점화식은 수열을 이웃에 있는 항과의 관계로 표현하는 것입니다.
이 때, 여러 수열이 몇 가지 관계식으로 연결된 것을 연립점화식이라고 합니다.
아래 그림과 같이 두 번째 층과 세 번째 층이 각각 3개, 2개의 유닛으로 구성되어있다고 가정해 봅시다.

두번째 층과 세번째 층은 다음과 같은 식으로 관계를 표현할 수 있습니다.
그러므로 두 번째 층과 세 번째 층은 연립 점화식으로 연결되어 있다고 할 수 있습니다.

시그마
시그마는 수열의 합을 나타낼 때 사용합니다.
간단하게 시그마를 이용한 수열의 합을 나타내보겠습니다.

시그마는 선형성이라는 특징이 있습니다.
그러므로 다음과 같은 규칙이 성립됩니다.

3. 벡터 (vector)
두 점 A, B에 대해서 A에서 B로 향하는 선을 선분(line segment)라고 합니다.
선분 중 방향을 갖는 선분을 유향 선분(directed segment)라고 합니다.
벡터(vector)는 이러한 선분의 방향과 크기만을 추상화한 것입니다.
벡터는 다음과 같이 좌표 평명에 나타낼 수 있고, 다음과 같이 표현할 수 있습니다.
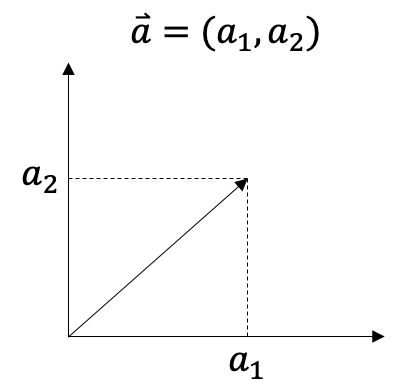
이 때, 좌표 평면에 나타난 선의 길이를 벡터의 크기라고 합니다.
벡터의 크기는 다음과 같이 구할 수 있습니다.

벡터의 내적
벡터의 내적은 "두 벡터가 어느 정도로 같은 방향을 향하고 있는가"를 나타낼 수 있습니다.
벡터의 내적은 다음과 같이 정의합니다.

코시-슈바르츠 부등식
코시-슈바르츠 부등식은 cosΘ의 값이 -1에서 1 사이의 값을 갖는 특징을 사용합니다.
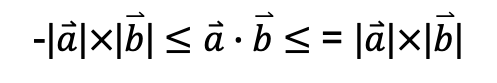
코시-슈바르츠 부등식은 두가지의 사실을 나타냅니다.
- 두 벡터가 반대 방향이면 두 벡터의 내적은 최소값을 갖습니다.
- 두 벡터가 같은 방향이면 두 벡터의 내적은 최대값을 갖습니다.
벡터의 내적은 다음과 같이 표현할 수 도 있습니다.
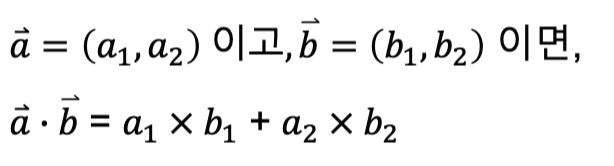
해당 식을 n차원으로 일반화한 경우 내적을 다음과 같이 나타낼 수 있습니다.

다시 유닛의 가중 입력으로 돌아가보면,
유닛의 가중입력 z는 다음과 같습니다.
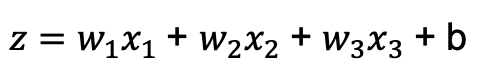
이 때, x벡터와 w벡터를 정의하면 가중입력 z는 다음과 같이 표현할 수 있습니다.
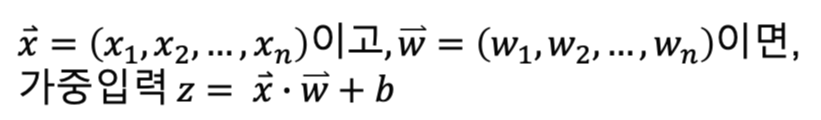
딥러닝을 이해하는데 도움이 될 수 있는 수학적인 개념은
다음 게시물에서 이어서 다뤄보도록 하겠습니다 :)
 |
|
<처음 배우는 딥러닝 수학>을 읽으면서 개인적으로 정리한 내용입니다.
제가 잘못 이해했거나, 수정이 필요한 부분에 대한 피드백은 언제든지 환영입니다.
감사합니다 :)
'필기 노트 > 처음 배우는 딥러닝 수학' 카테고리의 다른 글
| [딥러닝 기초] 오차역전법 (back-propagation) (0) | 2020.07.10 |
|---|---|
| [딥러닝 기초] 신경망과 학습 (0) | 2020.07.09 |
| [딥러닝 기초] 경사하강법과 회귀분석 (0) | 2020.07.09 |
| [딥러닝 기초] 딥러닝 수학 - 2 : 행렬, 미분 (0) | 2020.07.06 |
| [딥러닝 기초] 신경망과 딥러닝 개요 (0) | 2020.06.29 |




댓글