
Word2vec 논문을 읽다가 비교 대상으로 나온 Neural Network Language Model (NNLM)을 다룬 논문이다.
논문의 원본은 여기에서 볼 수 있다.
# 들어가기 전
논문을 직접 읽어보기 전에 먼저 어떤 내용인지, 공부한 내용을 기반으로 정리해보겠다.
이런거 필요 없이 논문 내용을 보고 싶다면 다음 섹션부터 읽으면 된다.
Neural Probabilistic Language Model (NPLM) 은 Distributed Representation을 사용하는 방식 중 하나이다.
기존에는 대부분 one-hot-encoding을 사용했다. One-hot-encoding에 대해서 간단하게 설명하자면, 전체 Vocabulary의 각 단어에 대해서 자신만의 인덱스를 부여한다. 각 단어의 word vector는 vocabulary 크기와 동일하게 생성되고, 해당 단어에게 부여된 인덱스의 값을 1로, 나머지 값들은 모두 0으로 표현하는 방식이다. 예를 들어, arsenal, chelsea, liverpool, manchaster로 구성된 volabulary가 존재한다고 했을 때, arsenal을 표현하기 위해서는 첫 번째 값을 1로 할당하고 나머지 값들은 모두 0으로 할당해서 표현하는 방식이다.

이런 식으로 표현하는 경우, 상당히 robust 하고 단순하다는 장점이 있지만, 다양한 단점들도 존재한다. 첫 번째로, 전체 vocabulary의 크기가 커지는 경우, 한 단어를 나타내는 단어 벡터의 크기도 함께 커진다는 것이다. 전체 단어 목록이 정말 커지는 경우, 한 단어를 표현하기 위한 벡터 또한 매우 커진다. 두 번째 단점으로는, 두 단어 사이의 관계를 표현하지 못한다는 것이다. 서로 다른 자리가 1로 되어 있고, 나머지 자리는 모두 0이기 때문에, 두 벡터를 내적하는 경우 무조건 0이 나온다. 두 벡터가 직교한다는 뜻인데, 이러면 두 벡터는 벡터 공간에서 서로 독립적으로 존재한다고 할 수 있다. 그러므로, one-hot-vector를 사용하는 경우 두 벡터 사이의 관계를 나타낼 수 없다. 두 번째 문제가 가장 큰 문젠데, 실제 생활 속에서는 단어들 사이에 관계가 존재하고, 그 관계를 표현하는 것이 매우 중요하기 때문이다. 이러한 문제들을 해결하기 위해서 distributed representation을 사용하게 된다.
NPLM에서는 여태까지 주어진 현재 단어를 이전 (n-1)개의 단어를 이용해서 예측하게 된다. 다른 말로 표현하면 $ t $ 번째 단어는 $ (t-1) $ 번째 단어부터 $ (t-n+1) $ 번째 단어를 기반으로 에측을 한다는 뜻이다. 이를 수식으로 쓰면 다음과 같다.
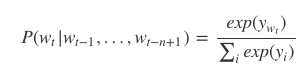
NPLM은 위의 조건부 확률을 최대화하는 방식으로 학습을 하게 된다. 이전의 (n-1) 개의 단어를 이용해서 현재 단어를 예측하기 때문에, n-gram 모델을 사용한다고 볼 수 있다.
[식-1] 에 대해서 더 이야기해보겠다. 위의 조건부 확률을 최대화하기 위해서는 분자를 최대화하고 분모를 최소화해야 한다. 식에 사용된 변수를 해석하면 다음과 같다.
- $ w_i $ : i 번째에 오는 단어
- $ y_{w_i} $ : $ w_i $ 에 해당하는 점수 벡터. 전체 vocabulary의 크기가 V 라고 하면, 해당 점수 벡터는 V-차원의 벡터로 구성된다.
NPLM의 출력층에서는 V-차원의 점수 벡터(score vector)에 해당하는 $ y_{w_i} $ 값을 softmax 함수를 통과시켜 나온 확률벡터를 제공한다. 확률 벡터에서 높은 확률값이 제공되는 인덱스의 단어가 (one-hot-vector를 사용하기 때문에) 실제 정답에 해당하는 단어와 일치하도록 학습을 진행한다.
NPLM의 입력층에서는 (n-1)개의 선행하는 단어들의 one-hot-vector가 입력으로 들어온다. One-hot-vector이기 때문에 각 벡터는 V-차원일 것이다. 각 벡터들은 $ C $ 와 연산을 통해서 지정된 크기인 $ m $ 차원의 입력 벡터로 변환된다. 해당 변환의 과정은 다음과 같다.

입력 벡터 $ x_t $가 m 차원이기 때문에, 해당 차원의 결과물을 만들어 내기 위해서 $ C $ 는 $ m \times |V| $ 의 차원을 보유하게 된다. One-hot-vector로 구성된 $ w_t $ 와 $ C $ 가 연산을 한다는 것은, $ C $ 행렬에서 t 번째의 열만 참조(lookup)하는 것과 동일한 연산이다.
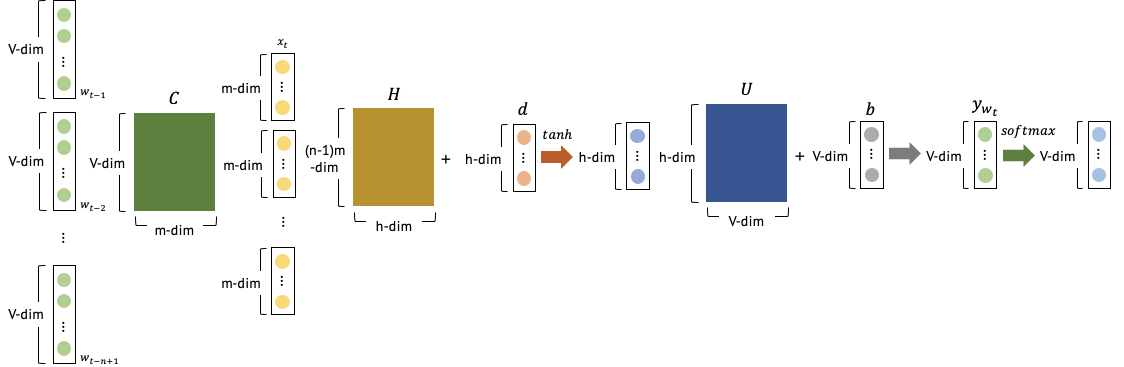
전체 과정을 순서대로 살펴보겠다. ([그림-1] 참고)
현재 단어 $ w_t $ 전의 (n-1) 개의 단어에 대한 one-hot-vector를 가져온다. 각 벡터는 V-차원으로 구성된다. V-차원의 (n-1) 개의 벡터는 공통으로 접근되는 C 를 통해서 m-차원의 (n-1)개의 벡터로 출력된다. 출력된 결과를 연결해서 입력 벡터인 $ x_t $ 를 생성한다. 해당 벡터는 (n-1)m-차원의 벡터로 구성된다. 입력 벡터는 hidden layer H 를 통과하고 d를 더해줘서 h-차원의 벡터를 생성한다. 결과로 출력된 벡터를 U와 연산을 하고, b를 더해주면 V-차원의 점수 벡터 $ y_{w_t} $ 가 출력된다. 점수 벡터는 softmax 함수를 통해서 확률분포를 제공한다. 점수 벡터를 구하는 식은 다음과 같다.

전체 NPLM 모델에서 사용되는 파라미터의 수는 다음과 같습니다.

NPLM 모델을 학습하는 과정에서 C, H, U, b, d 등 많은 파라미터들을 업데이트해야 하기 때문에 계산 비용이 크다는 단점이 있다. 이러한 단점을 극복하기 위해 제안된 것이 바로 word2vec 이다. (word2vec과 관련된 포스트를 읽어보려면 여기)
논문을 읽어보기 전에 NPLM이 대략 어떻게 동작하는지 조금 공부해봤고, 여기까지의 내용은 대부분 ratsgo's blog 에서 참고했다. 더 자세한 내용을 공부하려면 해당 블로그를 방문하는 것을 추천한다.




댓글