
CS224N의 6번째 강의, Language Model과 RNN에 대한 내용이다. 해당 강의는 여기에서 직접 들을 수 있다.
잘못된 내용, 궁금한 점, 피드백 모두 환영입니다 :)
주요 내용 : Language Modeling, RNN
# Language Modeling
이번 강의에서는 NLP의 대표적인 task 중 하나인 Language Modeling(LM)에 대해서 이야기한다. LM은 이전 단어들이 주어졌을 경우, 그다음으로 올 단어를 예측하는 문제이다. [그림-1]을 보면, "the students opened their"라는 단어들이 주어지고, 다음에 오는 빈칸에 어떤 단어가 가장 적합한지 예측하게 된다. 해당 그림에서는 books, laptops, exams, minds 등 다양한 예시를 제공하고 있다.

LM을 식을 이용해서 설명하면 [식-1]과 같이 설명할 수 있다. 해당 식을 위의 예시에 적용시켜 보면, $ x^1, x^2, x^3, x^4 $는 각각 the, students, opened, their에 해당하게 되고, 빈칸에 오는 단어는 $ x^5 $ 에 해당하게 된다. LM에서는 $x^1 ~ x^t $ 까지 주어졌을 때, 다음에 오는 단어인 $ x^{t+1} $ 이 나타날 확률을 구하게 된다.

우리가 예측하려는 단어 $ x^{t+1} $ 는 현재 존재하는 vocabulary 리스트 중에서 선택하게 되므로, classification task 라고도 볼 수 있다. LM을 이용해서 전체 text에 대한 probability를 계산할 수 있는데, 식은 다음과 같다.
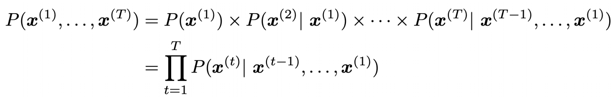
전체 텍스트를 구성하는 $ x^1 ~ x^T $ 가 나타날 확률은 각각 $ x^1 $ 만 나타날 확률 , $ x^1 $ 이 주어졌을 때 $ x^2 $ 가 나타날 확률 ,... , $ x^1 ~ x^{T-1} $ 이 주어졌을 때 $ x^T $ 가 나타날 확률의 전체 곱으로 나타낼 수 있고, 해당 값들은 LM을 통해서 구할 수 있다.
# n-gram Language Modeling
Deep learning 이전에 LM을 해결하기 위해서는 n-gram이라는 방법을 사용했다. n-gram 은 [그림-2]와 같이 연속적인 단어들의 모음이다. n-gram LM에서는 큰 corpus에서 해당 n-gram의 통계를 모두 구해서 해당 통계를 기반으로 다음에 나올 단어를 예측한다.

n-gram LM 에서는 Markov assumption이라는 전제를 기본으로 한다. Markov assumption은 (t+1) 번 째 오는 단어는 전체 텍스트에 의존적이지 않고, 이전에 오는 (n-1) 개의 단어에만 의존적이라는 것이다. 수식으로 표현하면 [식-3]으로 표현할 수 있다. 해당 확률은 단순히 (n-1)-gram 이 전체 corpus에서 몇 번 나타났는지, n-gram이 전체 corpus에서 몇 번 나타났는지를 count 해서 해당 값을 사용하게 된다.

[식-3]과 같이 n-gram을 이용해서 다음에 나타날 단어를 예측하는 경우 발생할 수 있는 문제는 크게 Sparsity probelm과 Storage problem 이 존재한다.
- Sparsity problem : [그림-3] 의 예시를 보자. 아래 예시는 4-gram으로 구성되어 있기 때문에, 빈칸에 들어가는 4개의 단어를 제외하고는 모두 고려하지 않는다. 이 4개의 단어를 봤을 때, 크게 두 가지 문제가 나타날 수 있다. 첫 번째로, 분모가 0이 되는 경우이다. 그 어떤 단어를 고려해도 "students opened their w"가 단 한 번도 corpus에서 나타나지 않은 경우이다. 이런 경우에는 Smoothing이라는 방식으로 해결하게 된다. Smoothing은 모든 단어에 대해 작은 count δ(delta)를 추가하게 된다. 그러므로, 모든 단어에 대해서 확률이 0이 발생하는 것을 막는다. 두 번째 더 심각한 문제는 분모가 0인 경우이다. w를 제외하고, "students opened their"라는 문구 자체가 한 번도 나타나지 않는 경우이다. 이런 경우 Back-off라는 방식으로 해결하게 된다. 이런 경우, 앞서 오는 (n-1) 개의 단어를 고려하는 것이 아니라, (n-2) 개의 단어를 사용하는 방식이다.
- Storage problem : 모든 n-gram에 대한 통계정보를 사용하기 때문에, 모든 n-gram에 대한 정보를 저장하고 있어야 한다. corpus가 커지고 n이 커질수록 저장해야 하는 크기가 커지게 된다.
# Fixed-window neural Language Modeling
n-gram LM이 위와 같은 문제들을 보유하기 때문에, 우리는 Neural Network를 이용해서 LM을 시도하게 된다. 다양한 방식 중 하나가 Fixed-Window neural Language Modeling이라고 한다. 해당 모델의 예시를 [그림-3]에서 볼 수 있다.
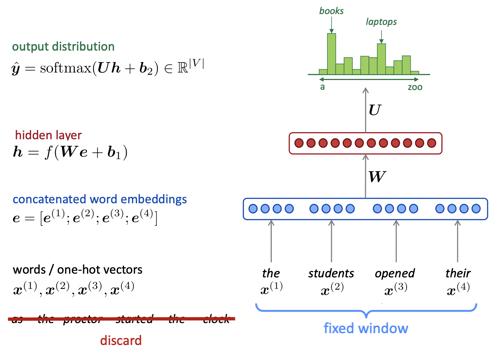
Fixed-window이기 때문에, fixed-window 밖의 단어들은 모두 고려하지 않는다. Fixed-window 내에 존재하는 단어들의 word embedding을 구하고, 해당 word embedding 을 연결한 벡터 e를 생성한다. 벡터 e를 hidden layer에 입력하고, 결과로 벡터 h를 제공한다. h는 최종적으로 softmax 함수의 입력으로 주어, 결과에 대한 확률분포를 제공하게 된다. 해당 확률분포는 가장 높은 확률로 다음에 올 단어를 예측하게 된다.
Fixed-window neural LM은 n-gram LM의 문제점들을 모두 해결한다. Sparsity problem과 storage problem 모두 해결하게 된다. 하지만 단점도 여전히 존재한다. 전체 문장에 대한 이해를 하기 위해서는 window-size가 아무리 커도 충분하지 않다는 것이다. 또한, 더 넓은 범위를 이해하기 위해서 window의 크기를 늘리는 경우, hidden layer W의 크기가 함께 커진다는 문제 또한 발생한다. 우리는 입력으로 들어오는 값의 길이에 구애받지 않고 처리할 수 있는 모델이 필요하게 되었다.
# Recurrent Neural Network (RNN)
Fixed-window neural LM의 문제점을 해결할 수 있는 모델이 바로 RNN이다. LM에서 RNN의 동작 방식을 [그림-4]를 통해서 설명하겠다.
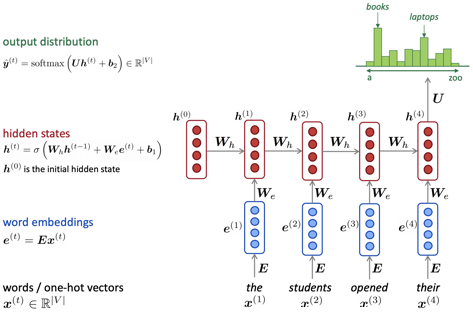
입력으로 들어오는 값은 $ x^1, x^2, x^3, ... $으로 길이에 상관없이 제공할 수 있다. 각 단어는 하나의 timestep에서 입력으로 제공된다. Timestep이 t라고 할 때, [그림-4]를 예시로 들면, t=1 일 때 "the"가 입력으로, t = 2 일 때 "students"가 입력으로 제공된다.
- 입력으로 들어온 단어는 해당 단어에 대한 word embedding으로 변환되고, $ W_e $ 와 연산을 하게 된다.
- RNN에는 hidden state가 존재하게 되는데, $ h^0 $ 은 initial hidden state로, zero-vector 또는 모델과 함께 학습되는 벡터를 사용한다고 한다. Initial hidden state는 $ W_h $ 와 연산을 하게 된다.
두 연산의 결과를 sigmoid 함수를 통해서 다음 timestep 의 hidden state인 $ h^1 $ 이 생성된다. 다음 timestep에서는 두 번째 단어 벡터인 "students"가 제공되고, 동일한 연산을 통해서 두 번째 hidden state 인 $ h^2 $ 가 생성된다. 마지막 단어에 대해서도 동일하게 연산이 진행되고, 최존 hidden state는 softmax 함수으 입력으로 제공되어 다음으로 나올 단어의 확률분포를 제공한다.
여기서 우리가 주목해야 하는 점은 전제 과정에서 우리는 동일한 $ W_h, W_e $ 를 사용한다는 것이다. 해당 matrix는 모든 timestep에 동일하게 적용된다는 것이다.
RNN의 학습은 Cross-entropy loss를 최소화하는 방향으로 진행된다. [그림-5] 처럼, 각 timestep 마다 모델이 예측한 값과 실제 정답(y)을 이용해서 손실 값 J를 구하게 된다. 모든 timestep에 대한 손실 값을 구하고, 전체 모델의 손실 값은 각 timestep의 손실 값의 평균을 이용하게 된다.
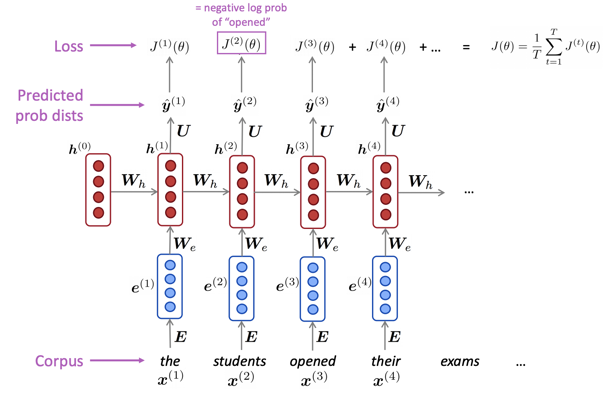
RNN을 이용해서 text generation을 할 수 있다. LM 과 동일한 방식으로 진행되는데, 한 가지 다른 점은, 한 timestep의 결과로 sampling 된 값을 다음 timestep의 입력으로 제공한다는 것이다. 이전에 생성된 단어를 입력으로 제공해서 다음 단어를 생성하는 방식으로 text generation을 진행할 수 있다.

RNN의 장/단점은 다음과 같다.
- 장점
- 입력 값의 길이에 상관 없이 처리할 수 있다.
- 이론적으로는 몇 단계 이전의 정보를 기억해서 결과에 반영할 수 있다.
- 입력의 길이가 길어져도 모델의 크기 ($ W_h, W_e $)는 변하지 않는다.
- 단점
- 연산 속도가 느리다. 이전 timestep의 연산을 완료해야 다음 timestep의 연산이 가능하기 때문에, 병렬 처리가 불가능하다.
- 실제로 사용했을 때, 과거의 내용을 그렇게 잘 기억하지 못한다.
RNN은 꼭 LM이 아니더라도 다양한 task에서 사용될 수 있다. Tagging task(POS, NER, etc.) , sentence classification(sentiment classification, etc.), text generation 등에 사용될 수 있다.
# Evaluating Language Model
LM은 perplexity를 이용해서 성능을 평가하게 된다. Perplexity에 대한 식은 다음과 같다.

[식-4]를 자세히 보면, 전체 copus의 probabilty의 역이라는 것을 알 수 있다. 1/T 를 통해서 normalization을 진행하는데, 단어가 많아지는 경우 perplexity가 작아지기 때문이다. 만약 LM이 좋은 성능을 제공한다면 낮은 perplexity를 제공하게 된다.

# Why do we care about LM?
LM 우리가 언어를 얼마나 잘 이해했는지에 대한 benchmark 로 사용할 수 있다. 또한, 다양한 NLP task의 subcomponent로 활용될 수 있다. NLP task로는 speech recognition, spelling/grammar correction, machine translation, summarization 등이 있다.
'대학원 이야기 > CS224N : NLP with Deep Learning' 카테고리의 다른 글
| [CS224N] Lecture 7 - Translation, Seq2Seq, Attention (수정 중) (0) | 2020.08.24 |
|---|---|
| [CS224N] Lecture 7 - Vanishing Gradients, Fancy RNNs (1) | 2020.08.23 |
| [CS224N] Lecture 5 - Dependency Parsing (0) | 2020.08.14 |
| [CS224N] Lecture 3 - Neural Networks (0) | 2020.08.12 |
| [CS224N] Lecture 2 - Word Vectors and Word Senses (0) | 2020.08.11 |




댓글