
CS224N의 7번째 강의, Vanishing Gradient와 다양한 RNN의 종류에 대한 내용이다. 해당 강의는 여기에서 직접 들을 수 있다.
잘못된 내용, 궁금한 점, 피드백 모두 환영입니다 :)
주요 내용 : Vanishing Gradient, RNN, LSTM, GRU, Bidirectional RNN, Multi-layer RNN
# Vanishing/Exploding Gradient
# Exploding Gradients
Back-propagation을 할 때 발생할 수 있는 문제 중 하나인 exploding gradient이다.

[식-1]을 보면 gradient와 learning rate을 이용해서 파라미터 값을 업데이트하는 식을 확인할 수 있다. 이때, gradient의 값이 너무 커지는 경우, 한 번에 큰 업데이트를 진행하게 되어서 Inf나 Nan과 같은 잘못된 결과를 제공할 수 있다. 이러한 문제점은 Gradient Clipping이라는 방식으로 해결할 수 있다.
Gradient clipping 은 일정 크기의 threshold 값을 지정해서, gradient 값과 threshold 값을 비교해서 gradient 값이 더 큰 경우 gradient 값을 감소시켜서 업데이트를 진행하는 방식이다. 동일한 방향으로 이동하면서 파라미터 값을 업데이트 하지만, 조금 더 작은 보폭으로 이동한다고 할 수 있다.

# Vanishing Gradients
Vanishing gradient는 gradient의 크기가 너무 작아지는 현상이다. RNN에서 vanishing gradient 가 어떤 문제를 발생시킬 수 있는지 확인해보겠다.
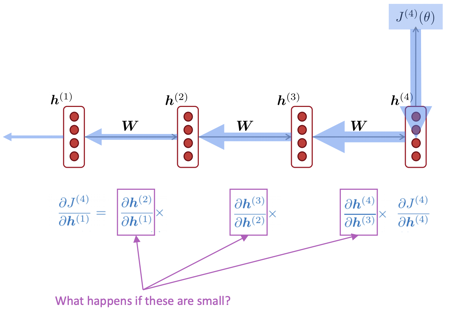
[그림-1]을 보면 back-propagation을 하는 과정을 볼 수 있다. 이러한 과정에서 chain rule을 이용해서 최종 미분 값을 구하게 되는데, 이때 문제가 발생하게 된다. 두 hidden state ($ h^t, h^{t+1} $) 사이의 미분 값을 구하게 되면 $ W_h $ 를 구할 수 있다. 모든 timestep 마다 동일한 $ W_h $ 를 사용하기 때문에, 모든 hidden state 사이의 미분 값은 동일하게 $ W_h $ 가 된다. 이때, $ W_h $ 의 크기가 너무 작아지는 경우, 작은 값끼리 곱하기 때문에 더욱 작은 값이 결과로 제공되고, 최종적인 gradient 값이 매우 작아지는 문제가 발생한다. 이러한 문제를 수식으로 표현하면 [식-3]처럼 표현할 수 있다.
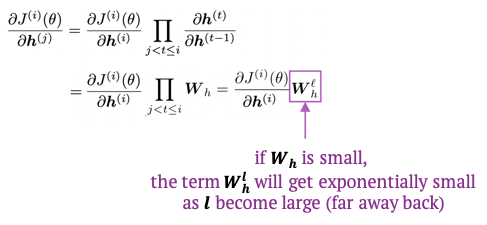
Gradient 값이 매우 작아지게 되는 현상은 RNN에서 [그림-2]와 같은 문제를 발생하게 한다.

위 그림에서 $ h^1 $ 의 관점에서 보겠다. $ J^2 $ 에 대한 gradient의 값은 $ J^4 $ 에 대한 gradient값 보다 훨씬 클 것이다. 그러므로, $ h^1 $ 은 $ J^2 $ 에 맞게 학습될 것이다. 다른 말로 표현하면, 파라미터들은 가까이에 위치한 dependency에 맞게 학습하고, 멀리 떨어진 dependency 에 대해서는 학습하지 못한다는 뜻이다.
Gradient 값이 너무 작아져서 0에 가까워지는 경우, 우리는 두 가지 판단을 해 볼 수 있다.
- 실제로 dependency 가 존재하지 않아서 0에 가까운 값으로 제공되는 경우
- dependency가 있지만, 파라미터를 잘못 설정해서 확인할 수 없는 경우
Gradient 값이 0에 가깝게 작아지는 경우, 우리는 위의 두 가지 경우 중 어떠한 이유 때문에 이러한 gradient 값이 구해졌는지 알 수 없다. 이러한 단점을 보유한 RNN을 Language Model (LM)에 적용하는 경우, 멀리 떨어진 단어들 사이의 dependency를 학습하지 못한다는 단점이 생기게 된다.

RNN의 이러한 문제는 [그림-3]과 같은 현장을 발생시킬 수 있다. LM task로 마지막 단어를 예측해야 하는 경우, 정상적인 답안은 writer 와의 dependency를 학습해서 "is"라는 결과를 제공하는 것이다. 하지만, RNN의 경우, 가까운 dependency를 더 잘 학습하기 때문에, sequential recency를 학습하게 되고, books 와의 dependency를 학습해서 "are"이라는 잘못된 결과를 제공하게 된다. RNN-LM은 이렇게 syntactic recency 보다, sequential recency를 더 빠르게 학습하게 되고, 그로 인해서 잘못된 결과를 제공할 수 있다.
과거의 내용을 잘 기억하지 못하는 RNN의 문제점을 별도의 메모리를 이용해서 해결한 것이 바로 그 유명한 Long-Short Term Memory (LSTM)이다.
# Long-Short Term Memory (LSTM)
RNN의 변형으로 기존의 hidden state와 함께 cell state를 사용한다. Cell state는 필요한 정보를 저장하기 위한 메모리라고 볼 수 있다. LSTM에서는 별도의 gate를 유지해서 cell state에 값을 읽을지, 쓸지, 지울지 판단하게 된다. gate의 값은 해당 timestep에서 입력으로 주어지는 input 값에 의존적으로 변하게 된다.
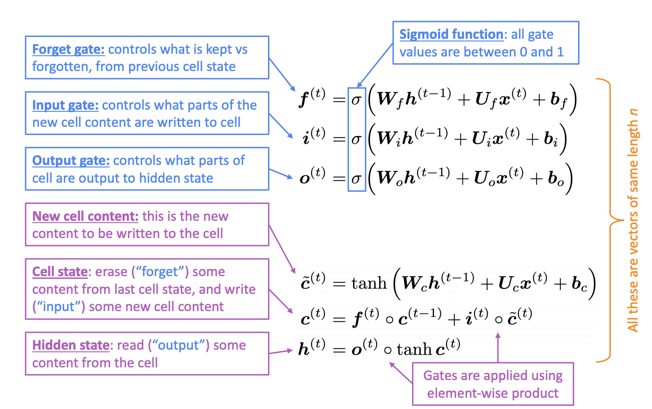
[식-4]는 LSTM의 한 timestep에서 수행되는 모든 연산이다.
- $ f $ (forget gate) : 이전 hidden state에서 어떤 값을 지울지 (forget), 어떤 값을 유지할지 판단한다.
- $ i $ (input gate) : 현재 timestep에서 입력으로 주어진 값 중 어떠한 값을 new cell content에 기록할지 판단한다.
- $ o $ (output gate) : cell state에서 어떤 값을 새로운 hidden state에 출력할지 판단한다.
- $ \widetilde{c} $ : 새로운 cell content에서 기록될 값
- $ c $ : 이전 cell state에서 유지되어야 할 값이 forget gate를 통해서 유지되고, 새로 생성된 cell content의 값 중 기록해야 할 값을 output gate를 통해서 기록된다.
- $ h $ : 새로 생성된 cell state를 output gate를 통해서 다음 timestep의 hidden state로 전달된다.
[식-4]를 그림으로 나타내면 다음과 같다.

LSTM의 cell state는 긴 timestep 동안 데이터를 유지할 수 있도록 도와준다. LSTM은 vanishing/exploding gradient을 완벽하게 예방하지는 못하지만 어느 정도 예방(?)할 수 있다.
# Gated Recurrent Unit (GRU)
LSTM이 너무 많은 연산으로 복잡하기 때문에, 이러한 복잡도를 낮추기 위해, Gated Recurrent Unit (GRU) 이 제안되었다. 기존의 LSTM과 다른 점은, cell state가 사라졌다는 것이다. Cell state을 사용하지 않고, hidden state에 정보를 계속해서 유지해나간다.

다양한 gated-RNN이 제안되었지만, LSTM과 GRU가 가장 많이 사용되고 있다. 해당 강의에서는 기본적으로 LSTM을 가장 먼저 사용하라고 추천한다. LSTM은 long-term dependency를 잘 학습하고, 데이터가 많은 경우 더 잘 학습한다고 한다. 하지만, LSTM의 동작이 너무 무겁거나, 적은 수의 파라미터를 원하는 경우 GRU로 바꿔서 사용하는 것을 추천한다. LSTM에 비해 GRU는 단순하고, 빠르고, 적은 파라미터 수를 보유하고 있기 때문이다. LSTM과 GRU 중 어떤 모델이 더 성능이 좋다고 명확히 판단하기는 어렵다고 한다.
# Other solutions to Vanishing Gradients
Vanishing Gradient 문제는 RNN 만의 문제가 아니다. 다른 feed-forward neural network, convolution network 등 다양한 모델에서도 발생하고, 깊게 모델이 구성될수록 더 심각하게 발생한다고 한다. Vanishing Gradient 문제를 해결하기 위한 다른 방법들도 제안되었다. 공통적인 특징은 이후에 나타나는 layer와 direct connection을 생성한다는 것이다. 대표적으로 ResNet과 DenseNet이 있다.
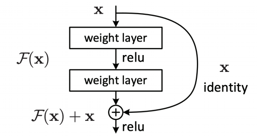
[그림-5]는 ResNet의 구조이다. ResNet의 경우, skip-connection을 이용해서 direct connection을 생성한다. 입력으로 들어오는 값 x를 convolution layer를 지나고 나온 결과에 더해줘서 과거의 내용을 기억할 수 있도록 한다.
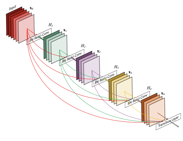
[그림-6]은 DenseNet의 구조이다. DenseNet은 이후에 나타나는 모든 layer에 대해서 direct connection을 생성한다.
# Bidirectional RNN
기존의 Vanilla RNN을 보면, 단방향으로 동작한다는 것을 알 수 있다. 그런데, 문장을 단방향으로 읽으면 문장 전체를 이해하는데 문제가 생길 수 있다. [그림-7]에 제시된 예시를 보자.

기존의 Vanilla RNN처럼 단방향으로 입력을 받는다면, "terribly"라는 단어를 먼저 접하게 되고, 그렇다면 문장 전체가 부정적인 문장일 것이라는 판단을 하게 된다. 하지만, 뒤에 오는 "exciting"이라는 단어 때문에 문장은 긍정적인 문장으로 해석된다. 이렇게 우리는 뒤에 오는 데이터를 함께 파악해야 하는 필요성이 생겼고, Bidirectional RNN은 그러한 역할을 수행한다. Forward RNN은 정방향으로 입력을 받아서 hidden state를 생성하고, backward RNN은 역방향으로 입력을 받아서 hidden state를 생성한다. 두 RNN이 생성한 hidden state를 연결해서 전체 모델의 hidden state로 사용하게 된다. 해당 동작을 식으로 표현하면 다음과 같다.
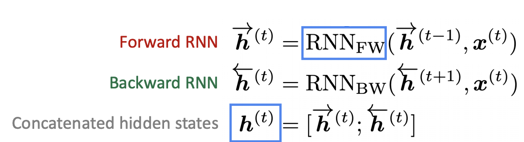
위의 식에서 사용되는 RNN은 그냥 vanila RNN을 사용해도 되고, LSTM, GRU와 같이 다양한 RNN의 종류를 사용해도 된다. Bidirectional RNN은 전체 입력 데이터를 보유하고 있는 경우 강력한 성능을 보여준다. 하지만, 전체 데이터가 없는 경우 사용할 수 없다. 그렇기 때문에 빈칸에 오는 단어를 예측해야 하는 Language Modeling에서는 사용할 수 없다.
# Multi-layer RNN
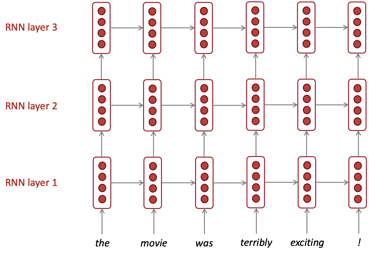
RNN도 여러 개의 층으로 사용할 수 있다. 여러개의 층으로 구성된 RNN은 더 복잡한 특성을 학습할 수 있다. 한 가지 예시를 들면 다음 그림과 같다. 여기에서 사용되는 RNN은 다양한 종류의 RNN을 모두 적용할 수 있다.
'대학원 이야기 > CS224N : NLP with Deep Learning' 카테고리의 다른 글
| [CS224N] Assignment 2 (1) | 2020.10.26 |
|---|---|
| [CS224N] Lecture 7 - Translation, Seq2Seq, Attention (수정 중) (0) | 2020.08.24 |
| [CS224N] Lecture 6 - Language Models and RNNs (0) | 2020.08.23 |
| [CS224N] Lecture 5 - Dependency Parsing (0) | 2020.08.14 |
| [CS224N] Lecture 3 - Neural Networks (0) | 2020.08.12 |




댓글